Data structure เนื้อหาไฟนอล 2566/1
October 31, 2023
Heap
- Max Heap
- Min Heap
Complete Binary Tree
- ทุกระดับ (Level) ของต้นไม้ (ยกเว้นระดับล่างสุดอาจจะไม่เต็ม) จะเต็มไปด้วยโหนด (Node)
- โหนดทั้งหมดในระดับล่างสุด (Last Level) จะอยู่ซ้ายสุด
Array implementation of Binary Tree
- การใช้ Array ในการเก็บข้อมูลของ Binary Tree โดยใช้ index ของ Array ในการเข้าถึงโหนดของต้นไม้ โดยใช้สูตรเพื่อหา index ของลูกโหนด (Child node) และ index ของ Parent
- Parent-child
- ถ้า idx เป็น Parent (idx เริ่มที่ 1)
- ถ้า idx เป็น Node นึงต้องการหา Parent (idx เริ่มที่ 1)
- parentIdx = idx / 2 (การหารปัดลง)
Heap implementation
- ต้องมีคุณสมบัติ (Propeties) สองข้อดังนี้
- ต้องเป็น Complete Binary Tree
- ค่าของ Parent ต้องมากกว่าหรือเท่ากับ ค่าของ Children (Max Heap) หรือ ค่าของ Parent ต้องน้อยกว่าหรือเท่ากับ ค่าของ Children (Min Heap)
Heap insertion
สามารถใส่ได้สองแบบ
-
Bottom Up (Shift Up)
-
ขั้นตอนการทำงาน (Max Heap) (idx เริ่มที่ 1)
-
Code
void insert(int x) { arr[tail] = x; tail += 1; heapifyBottomUp(tail - 1); } void heapifyBottomUp(int idx) { int parentIdx = idx / 2; if (parentIdx > 0) { if (arr[parentIdx] < arr[idx]) { swap(parentIdx, idx); heapifyBottomUp(parentIdx); } } }
-
-
Heapify (Build Heap) (Shift Down)
-
ขั้นตอนการทำงาน (Max Heap) (idx เริ่มที่ 1)
-
Code
void heapify(int idx) { int leftIdx = idx * 2; int rightIdx = idx * 2 + 1; int largestIdx = idx; if (leftIdx < tail && arr[leftIdx] > arr[largestIdx]) largestIdx = leftIdx; if (rightIdx < tail && arr[rightIdx] > arr[largestIdx]) largestIdx = rightIdx; if (largestIdx != idx) { swap(idx, largestIdx); heapify(largestIdx); } }
-
Heap deletion
-
ขั้นตอนการทำงาน (idx เริ่มที่ 1)
-
Code
int remove() { int x = arr[1]; swap(1, tail - 1); tail -= 1; heapify(1); return x; }
Priority Queue
- มีการทำงานคล้าย Queue ธรมมดา แต่ข้อมูลแต่ละอันจะมี Priority หรือลำดับความสำคัญ
- โดยที่ข้อมูลที่มี Priority สูงสุดจะถูก Dequeue ก่อน
Heap Sort
-
เป็นอัลกอริทึมการเรียงที่สร้างมาจาก Binary Heap
-
หลักการทำงาน (Max Heap)
- จาก Array ที่เข้ามาจะทำการ Build Heap ซึ่งจะได้ตัวแรกเป็นค่าที่มากที่สุด
- ลูปจนกว่า Heap จะว่าง
- นำ Max ของแต่ละครั้ง ไปใส่ไว้ด้านท้าย
- ทำการ heapify
-
Code
// https://www.geeksforgeeks.org/heap-sort/ void heapSort(int arr[], int N) { // Build heap (rearrange array) for (int i = N / 2 - 1; i >= 0; i--) heapify(arr, N, i); // One by one extract an element // from heap for (int i = N - 1; i > 0; i--) { // Move current root to end swap(arr[0], arr[i]); // call max heapify on the reduced heap heapify(arr, i, 0); } }
Binary Tree
- เป็น Tree ที่มี Children อย่างมาก 2 Node (0, 1, 2)
- Left subtrees
- Right subtrees
- Node:
- Children:
- Root: ยอดต้นไม้
- Degree: จำนวน Children
- Sibling: Node ที่่มี Parent เดียวกัน
- Leaf node: Node ที่ไม่มี Children หรือ degree เป็น 0
- Internal node: Node ที่ไม่เป็น Leaf node
- Ordered tree: จะถูกจัดเรียงตามลำดับที่กำหนดไว้ เช่น Binary Search Tree, AVL Tree
- Unordered tree: ข้อมูลในต้นไม้จะไม่ถูกจัดเรียงตามลำดับใด ๆ ข้อมูลใด ๆ ก็สามารถอยู่ตำแหน่งใดก็ได้ในต้นไม้
- Path: คือเส้นทางของ Node
- เช่น B, E, G ความยาว (n) คือ 2

- เช่น B, E, G ความยาว (n) คือ 2
- Descendants: ลูกๆ หลานๆ
- เช่น Descendant ของ B คือ B, C, D, E, F, G

- เช่น Descendant ของ B คือ B, C, D, E, F, G
- Ancestors: บรรพบุรุษ
- เช่น Ancestor ของ I ของ I, H, A

- เช่น Ancestor ของ I ของ I, H, A
- Predecessor
- Successor
Tree Height
- ความสูงของต้นไม้จะเป็น ระยะทางสูงสุดจาก Root ไปยัง Node ใด ๆ ในต้นไม้
- ความสูงของต้นไม้ที่มี Node เดียวคือ 0 (เฉพาะ Root Node)
- ต้นไม้เปล่า ความสูงเท่ากับ -1
Tree Depth
- จำนวน Edge จาก root ไป Node นั้นๆ
- เช่น
- E มี Depth เท่ากับ 2
- L มี Depth เท่ากับ 3
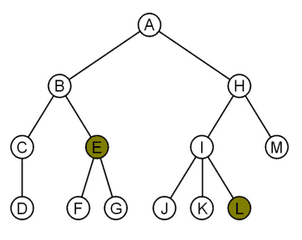
Full Binary Tree
- ทุกระดับ (Level) ของต้นไม้เต็มไปด้วยโหนด
- ทุกโหนดยกเว้นปมใบ (Leaf Node) จะมีลูกโหนด 2 ลูก (Children)
Traversal
- Breadth-first traversal
- เดินให้ครบทุก Node ในความลึก ก่อนจึงไปเดินต่อที่ความลึก
- Queue
- Depth-first traversal
- เดินให้ลึกที่สุดก่อน จึงจะไปเดิน Sibling อื่นๆ
- Stack / Recursive
- Preorder / Inorder / Postorder traversal
- Preorder: root left right
- Inorder: left root right
- Postorder: left right root
Binary Search Tree
- คุณสมบัติ (Properties)
BST Insertion
-
หลักการทำงาน
- เดินจนกว่าจะเป็น Empty BST หรือ null
- ใส่ newNode
-
Code
BST *insert(BST *root, int x) { // Reached the leaf node if (root == NULL) return new BST(x); if (x < root->val) root->left = insert(root->left, x); else if (x > root->val) root->right = insert(root->right, x); return root; }
Predecessor and Successor
- Inorder Predecessor คือค่าที่น้อยกว่าค่า target
- Inorder Successor คือค่าที่มากกว่าค่า target
BST Deletion
-
จะเป็น ถ้าเป็น Perfect Binary Tree
-
หลักการทำงาน
- หา Node ที่จะลบ
- แบ่งการลบออกเป็น 2 เคส
- Zero or one child: จะลบออก และแทนที่ด้วย Children ของมัน
- ถ้า เป็น null ให้ลบตัวนั้นและ return แทน
- ถ้า เป็น null ให้ลบตัวนั้นและ return แทน
- Two children
- หา Node ที่จะลบ
- สลับค่าของ ตัวที่จะลบกับ Successor
- เรียกฟั่งชั่น ลบ
- Zero or one child: จะลบออก และแทนที่ด้วย Children ของมัน
-
Code
BST *remove(BST *root, int x) { if (root == NULL) return root; // search for the node to be deleted // after those line, root will be the node to be deleted if (x < root->val) { root->left = root->remove(root->left, x); return root; } else if (x > root->val) { root->right = root->remove(root->right, x); return root; } // case 1 and 2 (zero or one child) if (root->left == NULL) { BST *tmp = root->right; delete root; // return to the parent return tmp; } else if (root->right == NULL) { BST *tmp = root->left; delete root; // return to the parent return tmp; } // case 3 (two children) else { // find successor in the right subtree BST *tmp = find_minimum(root->right); // copy the successor's value to the current node root->val = tmp->val; // delete the successor root->right = root->remove(root->right, tmp->val); return root; } } // successor BST *find_minimum(BST *root) { while (root->left != NULL) root = root->left; return root; }
AVL
- คุณสมบัติ (Properties)
- เป็น Self-Balancing BST
- มีการปรับโครงสร้างระหว่างทำงาน
- มีความสูงของ Children ซ้าย กับ ขวา ได้ไม่เกิน 1 ()
- เป็น Self-Balancing BST
- จะมีความสูง เสมอ
Tree Rotating
- Left Rotate
-
หลักการทำงาน x = root
- ทางขวาของ root (x) จะเป็น root อันใหม่ (y)
- root อันเดิมมาเป็นด้านซ้ายของ root อันใหม่ y->left = x;
- ทางซ้ายของ root ใหม่ (y) มาเป็นทางขวา ของ root เก่า
-
Code
Node *leftRotate(Node *x) { Node *y = x->right; Node *T2 = y->left; // Perform rotation y->left = x; x->right = T2; // Update heights x->height = max(height(x->left), height(x->right)) + 1; y->height = max(height(y->left), height(y->right)) + 1; // Return new root return y; }
-
AVL Balancing
-
หลักการทำงาน
- อัพเดตความสูงใหม่
- ความสูง = 1 + max(ความสูงของ Left child, ความสูงของ Right child)
- เช็คว่า Balance ไหมจาก
- ผลต่างความสูงของ Left child และ ความสูงของ Right child มากกว่า 1
- อัพเดตความสูงใหม่
-
Code
node->height = 1 + max(height(node->left), height(node->right)); // height(node->left) - height(node->right) int balance = getBalance(node); // Left Left Case if (balance > 1 && key < node->left->key) return rightRotate(node); // Right Right Case if (balance < -1 && key > node->right->key) return leftRotate(node); // Left Right Case if (balance > 1 && key > node->left->key) { node->left = leftRotate(node->left); return rightRotate(node); } // Right Left Case if (balance < -1 && key < node->right->key) { node->right = rightRotate(node->right); return leftRotate(node); } /* return the (unchanged) node pointer */ return node;
AVL Deletion
- หลักการทำงาน
- ทำการ BST Deletion
- ทำการ AVL Balancing
ถ้า Balance ของขั้นที่ 2 เท่ากัน หรือ ให้ดูจากขั้นที่ 1
Graph
Definition นิยาม
- ประกอบด้วยเซ็ตของ Node / Vertices (V) และเซ็ตของ Edge / Arcs (E)
- ไม่มีการจัด Level
- จะเขียนเป็นคู่ลำดับ
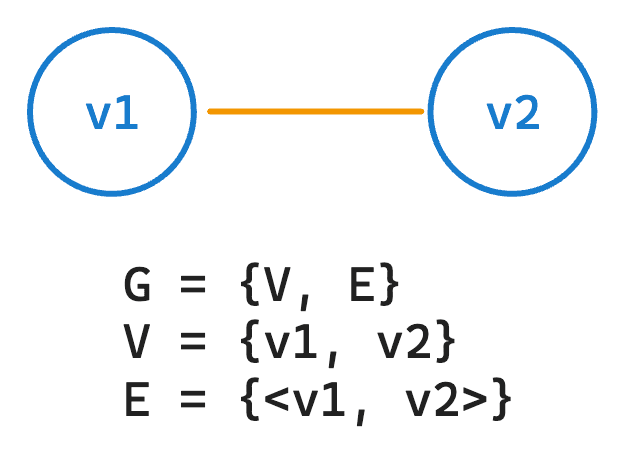
- กราฟที่มีทิศทาง: จะมีความสำคัญว่าสลับได้ไหม
- Directed: มีทิศทาง มีลูกศร
- Undirected: ไม่มีทิศทาง ไม่มีลูกศร
- ถ้าเรียกว่า Graph ปกติ จะเป็นกราฟที่ไม่มีทิศทาง (Undirected)
- Directed Graph => Digraph (ชื่อเล่น)
- Adjacent: อยู่ชิด / ติดกัน
- W จะ adjacent กับ V ถ้า
- หลัง จะ adjacent กับ หน้า ถ้า
- ถ้าเป็นกราฟไม่มีทิศทาง แล้ว แสดงว่า ด้วยและ
- V adjacent กับ W
- W adjacent กับ V
- Weight หรือ Cost คือตัวเลขที่อยู่บน Edge
- Parallel Edge: เส้นขนาน
- Loop: กราฟวน
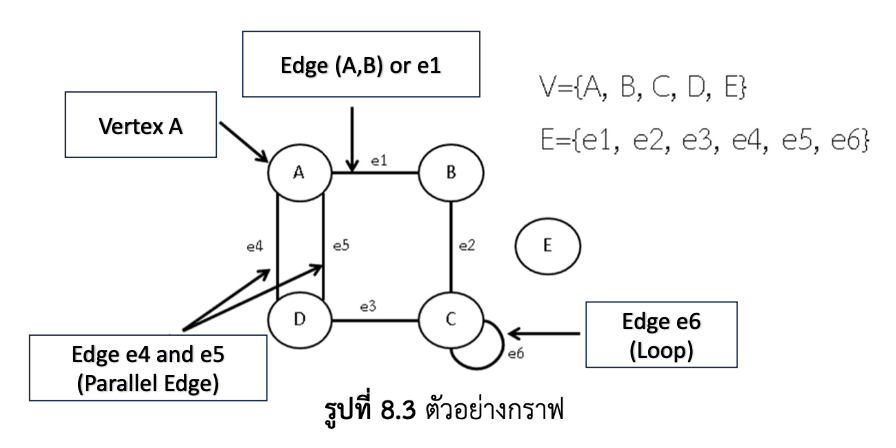
- Simple graph: กราฟปกติ
- Complete graph หรือ Mesh: กราฟที่เชื่อมกันทุกสาย
- Walk: เป็นระดับการสำรวจของ Vertices และ Edge
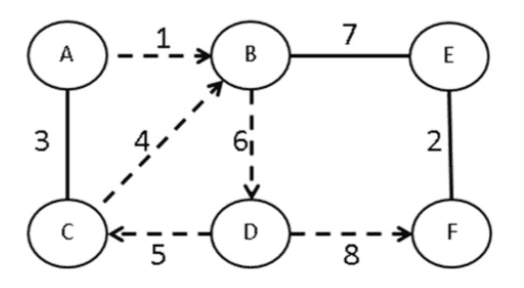
- Trail: เป็นการเดิน (Open Walk) ไม่วน Edge เดิม
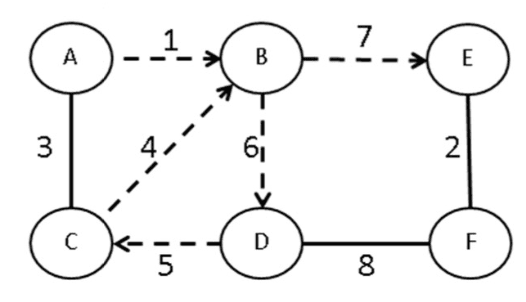
- Circuit: เดินวนกลับมาที่จุดเริ่มต้น แต่จะไม่เดินซ้ำ Edge เดิม (Closed Trail)
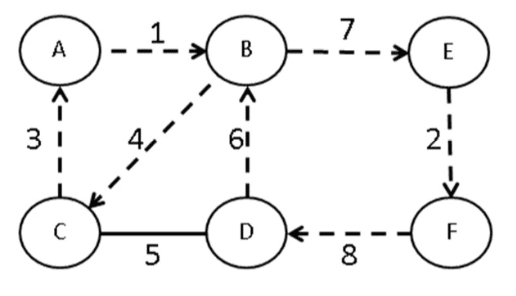
- Path: ห้ามเดินซ้ำ Edges และ Vertices
- Cycles: จุดเริ่มต้นและจุดจบเหมือนกัน แต่จะไม่เดิน Edges และ Vertices ซ้ำกัน
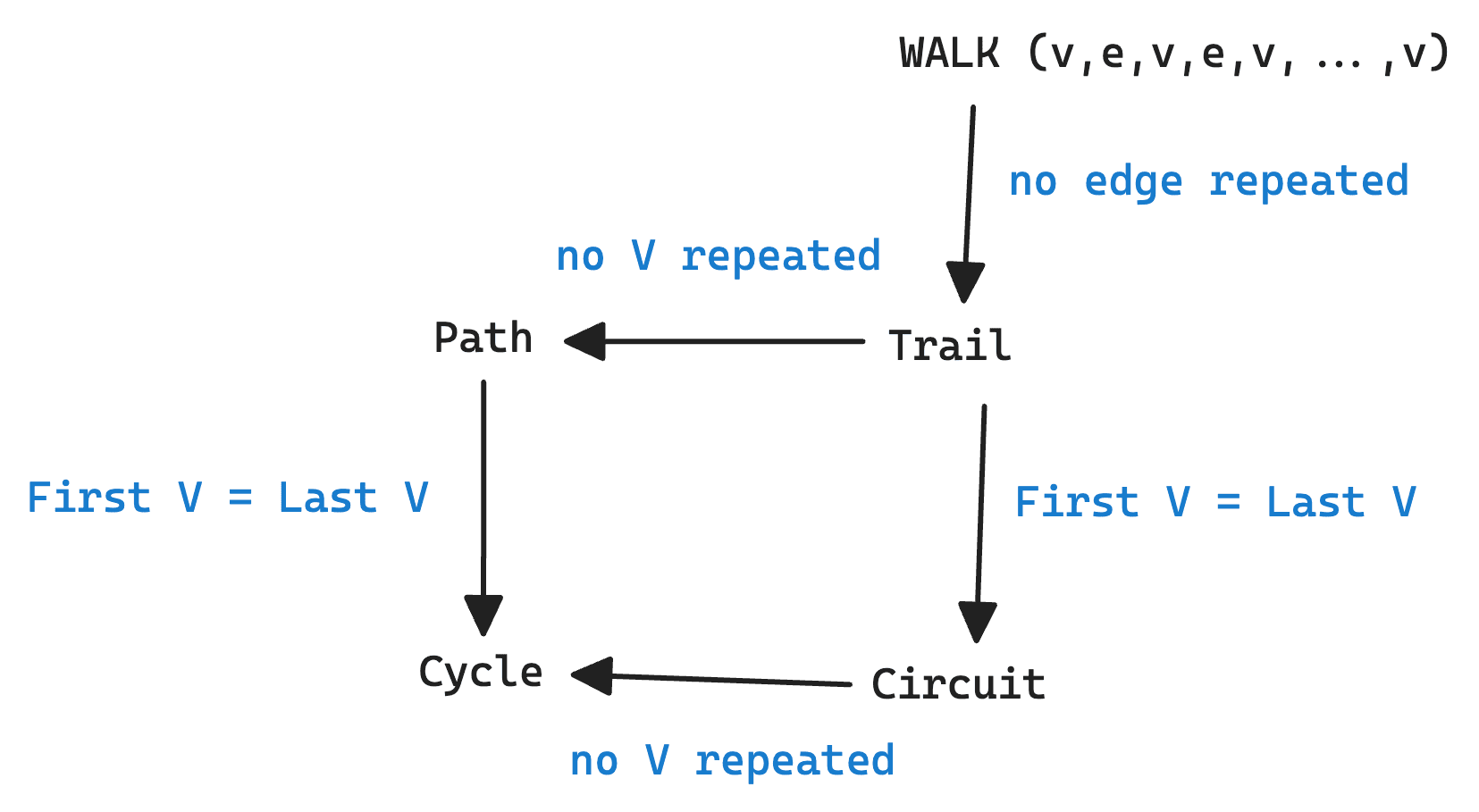
- Connected Graph: ทุกตัวสามารถเดินถึงกันได้หมด
- Island หรือ Components: คือ Sub graph หรือ ไม่ใช่ Connected Graph
- Subgraph: Subset ของ Graph
- Type of Graph
- Unweighted undirected graph หรือ Graph
- Unweighted directed graph
- Weighted undirected graph
- Weighted directed graph
- Degree: จำนวนเส้นที่ชี้ออกจากจุดนั้นๆ
- Odd Degree: คี่
- Even Degree: คู่
- In degree: จำนวนเส้นที่เข้า
- Out degree: จำนวนเส้นที่ออก
Application
- นำมาอธิบายความสัมพันธ์ของข้อมูลต่างได้ เช่น
- Transportation: Google Maps
- Social Networks
- Internet and Network
- แต่เนื่องจากคำนวน Graph ใช้เวลาและ Resource ที่เยอะมาก บางทีอาจจะเลือกข้อมูลมาเป็น Tree
Representation วิธีการเก็บ
-
Adjacency Matrix: Two dimesions array
- Undirected: Symmetric matrix
- Directed: ส่วนมากจะเริ่มจาก Row เป็น Source ไป Column เป็น Destination

โดยที่ขนาด Matrix จะเท่ากับ จำนวน Node x จำนวน Node เหมาะสำหรับข้อมูลขนาดที่รู้อยู่แล้ว หรือไม่ใหญ่มาก
-
Adjacency List: Linked Lists
| Source | Destination |
|---|---|
| 1 | 2, 4, 3 |
| 2 | 4, 5 |
| 3 | 6 |
| 4 | 6, 7, 3 |
| 5 | 4, 7 |
| 6 | (empty) |
| 7 | 6 |
Operations
- Add vertex
- Delete vertex ต้อง delete edge ด้วย
- Add edge
- Delete edge ลบได้เลย
Graph Traversal
- ต้องสามารถเดินได้ครบทุกคน
- ต้องไม่มีการประมวณผลซ้ำ
- Depth First Search (DFS): ลึก
- ทุกครั้งที่เดินต้องเป็น Edge ใหม่, Vertices ใหม่, ต้องไกลขึ้นเรื่อยๆ
- Breadth First Search (BFS): กว่าง
- Tree Edges เป็น edge ที่ใช้เดินผ่านใน DFS หรือ BFS
- Back edges เป็น edge ที่ไม่ได้นำมาใช้ใน DFS หริอ BFS (สำหรับ Undirected)
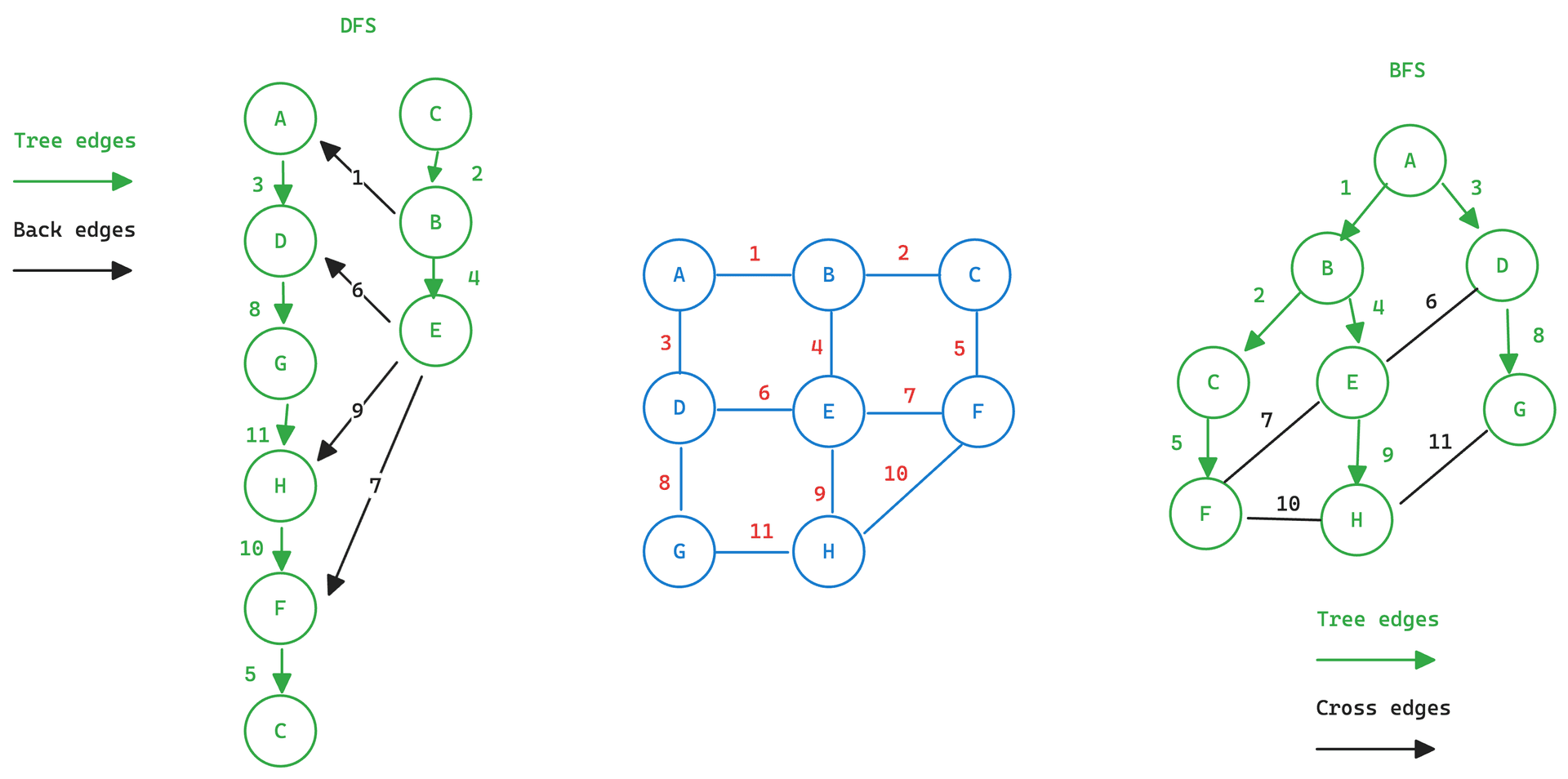
| Algorithm | Type of graph | Type of the edges |
|---|---|---|
| Depth first search | Undirected | Tree Edges + Back Edges |
| Breath first search | Undirected | Tree Edges + Cross Edges |
| DFS, BFS | Directed | Tree Edges, Back Edges, Cross Edges, Forward Edges |
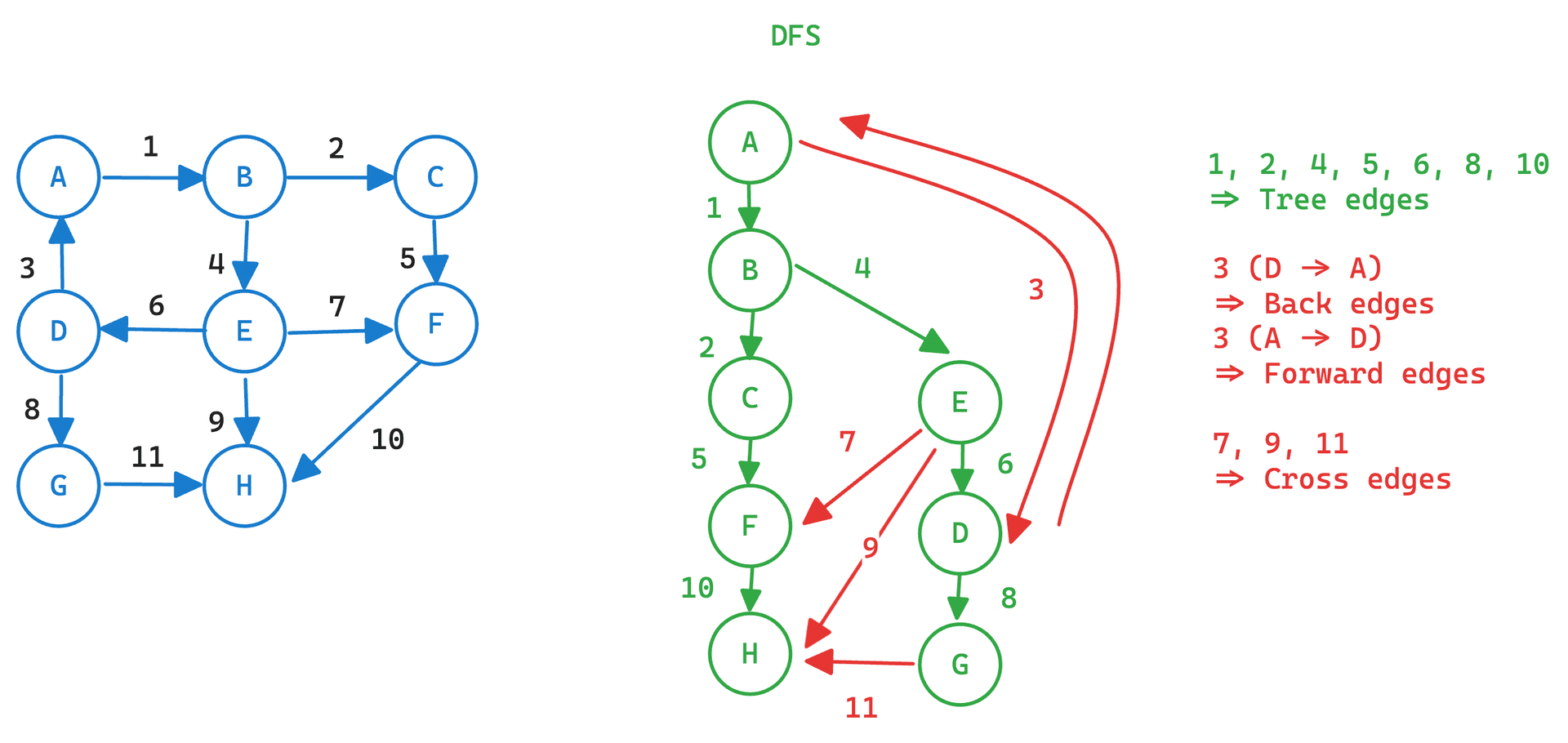
- Forward / Back edges จะเป็น Edges ที่อยู่ใน Path เดียวกัน (สำหรับ Directed)