Data structure เนื้อหามิดเทอม 2566/1

August 31, 2023

by Athicha Leksansern

Why should we learn Data structure?
Chapter 1 Data structure
Chapter 2 Stacks
Chapter 3 Queue
Chapter 4 Linked list
Chapter 5 Hash table

Why should we learn Data structure?

I have a data, what data structure can it represent
- Definition, Draw, Explain
How can i input that data to its structure
How can i process that data for wanted result

Chapter 1 Data structure

Type of Data structure

Primative data structure: Anything with single value
- ex. int, char, float, long, double, and pointer
Non-primative
- Linear: array, linked list, stack, queue
- Non-linear: tree, graph

Memory allocation

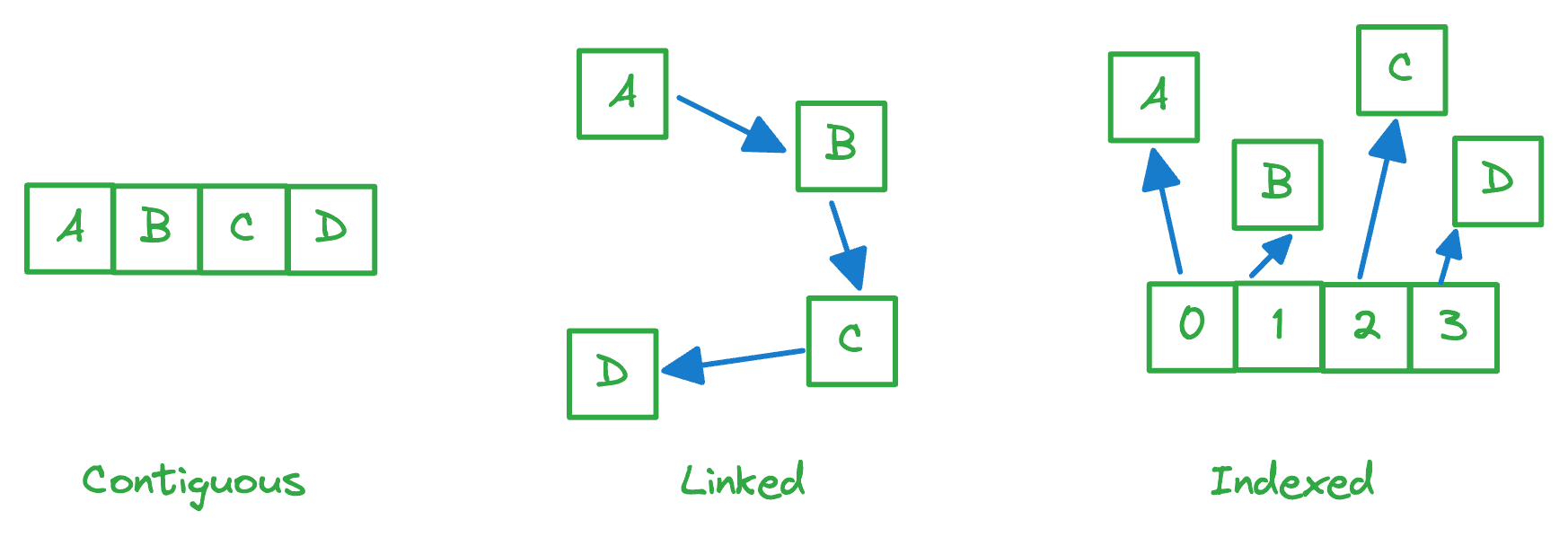
Contiguous
- An array stores n objects in a single contiguous space of memory
Linked
- The object itself, and
- A reference to the next item
Indexed
- An array of pointers

Type of problems

Non computable Problem – It can not be transformed into mathematic function.
- It can not be used computer to solve this type of problem.
Computational Problem – can be transformed into mathematic function.
- We can use computer to solve this type of problem.

Complexity

Space complexity: Amount of memory space
Time complexity: Analysis performance of run time

Landau Symbols คือ Big O Notation

Chapter 2 Stacks

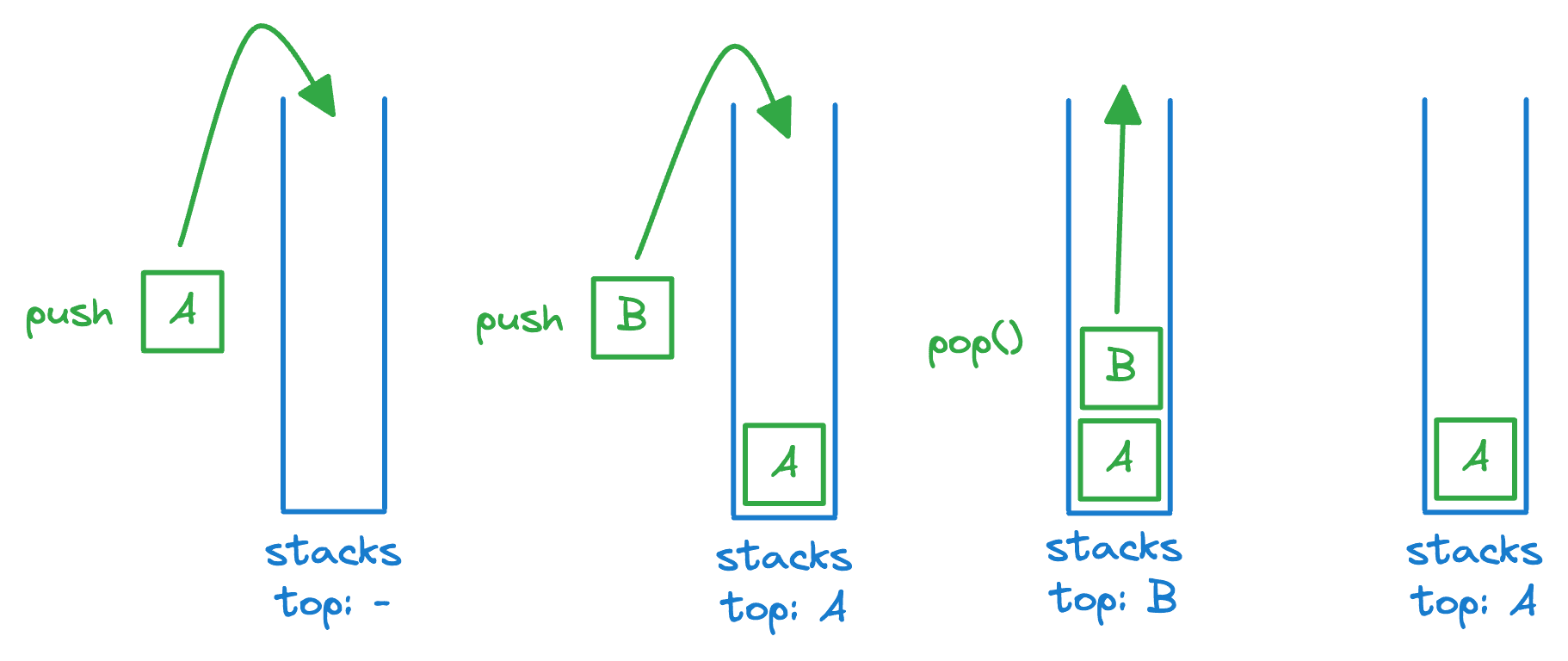
What is a stack?

Last-In-First-Out (LIFO)
Uses a explicit linear ordering
Insertions and removals are performed individually
push: Inserted objects are pushed onto the stack
top: The top of the stack is the most recently object pushed onto the stack
pop: When an object is popped from the stack, the current top is erased

Constructor and Destructor

Constructor: Run when object is created
Destructor: Run when object is removed or not used

class Stack {
    public:
        Stack() {
          // Constructor
        }
        ~Stack() {
          // Destructor
        }
};

Stack Implementations

Using array

For one-ended arrays, all operations at the back are $O(1)$

class Stack {
    private:
        int arr[10];
        int top_idx = 0;
    public:
        bool empty() {
            return top_idx == 0;
        }
        int top() {
            return arr[top_idx - 1];
        }
        void push(int val) {
            arr[top_idx] = val;
            top_idx += 1;
        }
        void pop() {
            top_idx -= 1;
        }
}

Using Linked list

class Node {
    public:
        char val;
        Node* next;
};

class Stack {
    private:
        Node *head = NULL;
    public:
        void push(char val) {
            // Insert First
            Node *new_node = new Node();
            new_node->val = val;
            new_node->next = head;

            head = new_node;
        }
        bool empty() {
            return head == NULL;
        }
        void pop() {
            // Delete First
            Node *tmp = head;
            head = head->next;

            delete tmp;
        }
        char top()  {
            return head->val;
        }
};

Using C++ STL library

#include <iostream>
#include <stack>
using namespace std;
int main() {
    stack<int> mr_stack;
    mr_stack.push(21);
    mr_stack.push(25);
    mr_stack.push(17);
    mr_stack.pop();
    while (!mr_stack.empty()) {
        // 25 21
        cout << mr_stack.top() << " ";
        mr_stack.pop();
    }
    return 0;
}

Stack Applications

Parsing code:
- Matching parenthesis
- XML (e.g., XHTML)
Tracking function calls
Dealing with undo/redo operations
Reverse-Polish calculators
Assembly language
ปัญหาอะไรก็ตามที่
1. ทำแล้วเจอปัญหาย่อย
2. เมื่อปัญหาย่อยเสร็จต้องกลับไปทำปัญหาเดิม
Fucking Reverse-Polish Notation

Chapter 3 Queue

What is a queue?

First-In–First-Out (FIFO)
enqueue: Inserted objects are pushed onto the queue
dequeue: The top of the queue is the least recently object (oldest) pushed onto the queue
top หรือ front: The top of the queue is the least recently object (oldest) pushed onto the queue

Queue Implementations

Using array

class Queue {
     private:
         int arr[10];
         int front_idx = 0;
         int back_idx = 1;
         int queue_count = 0;
     public:
         bool empty() {
             return queue_count == 0;
         }
         int top() {
             return arr[front_idx % 10];
         }
         void enqueue(int val) {
             queue_count += 1;
             
             arr[(back_idx - 1) % 10] = val;
             back_idx += 1;
         }
         void dequeue() {
             queue_count -= 1;
             front_idx += 1;
         }
 };

Using Linked list

class Node
{
public:
    int val;
    Node *next;
};

class Queue
{
public:
    Node *head;
    void enqueue(int val)
    {
        // Insert last
        Node *new_node = new Node();
        new_node->val = val;
        new_node->next = NULL;

        if (head == NULL)
        {
            head = new_node;
        }
        else
        {
            Node *tmp = head;
            while (tmp->next != NULL)
            {
                tmp = tmp->next;
            }
            tmp->next = new_node;
        }
    }
    void dequeue()
    {
        // Removed first
        Node *tmp = head;
        head = head->next;
        delete tmp;
    }
    int top()
    {
        // First position
        return head->val;
    }
    bool empty()
    {
        return head == NULL;
    }
};

Using C++ STL library

#include <iostream>
#include <queue>
using namespace std;
int main()
{
    queue<int> mr_queue;
    mr_queue.push(10);
    mr_queue.push(20);
    mr_queue.push(30);
    mr_queue.pop();
    while (!mr_queue.empty()) {
           // 20 30
           cout << mr_queue.front() << " ";
           mr_queue.pop();
    }
    return 0;
}

Queue Applications

อะไรที่ต้องรอคิว
Breadth-first traversal in Binary Tree
- เดินในชั้นนั้นให้ครบก่อน แล้วจึงข้ามไปชั้นต่อไป
- Steps
  1. ให้ root อยู่ Queue
  2. loop จนว่า Queue จะว่าง
    1. เอา top() ออกมาตั้งเป็น current
    2. current เป็นผลลัพท์
    3. dequeue() top ทิ้ง
    4. ถ้ามี current ตัวขวานำมาใส่ Queue
    5. ถ้ามี current ตัวซ้ายนำมาใส่ Queue

Chapter 4 Linked list

A linked list is a data structure where each object is stored in a node
As well as storing data, the node must also contains a reference/pointer to the node containing the next item of data

class Node {
    public:
        char val;
        Node* next;
};

Static Allocation vs Dynamaic Allocation

// Static Allocation
int f() {
    // Object is created in the local scope in the func
    Node new_node;
    new_node.val = 555;
    cout << new_node.val << endl;
    // After the function is return
    // C++ Will call class destructur and destroy new_node (which is local variables) 🎇🎇
    return 0;
}

// Dynamaic Allocation
int f2() {
    Node *new_node = new List();
    new_node->val = 555;
    cout << new_node->val << endl;
    // After the function is return
    // The object will still be in the memory F O R E V E R
    return 0;
}

Linked list Operations

Insert into
Access
Erase from

ผมแนะนำให้เพื่อนหยิบปากกามาวาดทีละขั้นตอนว่าควรทำอะไรก่อนอะไรหลัง เดินตามเส้น Pointer ไปเรื่อยๆ เพื่อไม่ให้เส้นขาด เทคนิคก็คือส่วนมากมักจะแก้ที่ Node ใหม่ก่อน สู้ๆ ครับ ^ ^

Doubly linked list

class Node {
    public:
        char val;
        Node* next;
        Node* prev;
};

Chapter 5 Hash table

Searhing

Linear Search: search data in linear data structure
- Sequential Search: หาทีละอัน
- Binary Search: ทาทีละครึ่ง
- Index Sequential Search: หาตามกลุ่ม
  - เช่น สารบัญ เรื่องเกี่ยวกับ ... อยู่หน้า 12 - 42
- Hash Search

What is a hash table?

Hash table หรือเรียกอีกอย่างว่า Hash map เป็น Data structure ที่สามารถเชื่อมค่า Key ไป Value ได้
Hash table ใช้ Hash function เพื่อคำนวนสื่งที่เรียกกว่า Index (หรือ Hash code) เพื่อนำไปเป็น Index ใน Array ทำให้สามารถเก็บ / ดึงค่าออกมาได้
ระหว่างการหาค่าใน Hash table, Key จะถูก Hashed และผลลัพท์ของ Hashed Key จะนำไปสู่ตำแหน่งของ Value ได้
รวม Code ของ Hash table

Hash function

Direct Hashing
- นำ Key มาเป็น Index index = key;
Subtract Hashing
- นำ Key มาลบด้วยบางค่า index = key - SUBTRACT;
Digit-Extraction Hashing
- ใช้บางส่วนของเลขมาเป็น index
- เช่น ${\color{red}1}234{\color{red}5}678{\color{red}9}$ ใช้ตำแหน่งที่ 1, 5, 9 จะได้ $\text{index} = 159$
Mid Square Hashing
- นำ Key มากำลังสองและเอาค่าตรงกลางของผลลัพท์มาเป็น Index
- เช่น $\text{Key} = 425 \rArr 245^2 \rArr 18{\color{red}06}25,\text{index} = \color{red}{06}$
Fold Shift Hashing
- แบ่ง Key ออกเป็น 3 ส่วน (a, b, c)
- เอามารวมกันแล้ว mod HASH_SIZE
- index = (a + b + c) % HASH_SIZE;
Fold Boundary Hashing
- แบ่ง Key ออกเป็น 3 ส่วน (a, b, c)
- reverse เลขซ้าย และ เลขขวา
- index = (reverse(a) + b + reverse(c)) % HASH_SIZE;
- เช่น $123456789 \rArr {\color{red}123},456,{\color{red}789} \rArr {\color{red}321} + 456 + {\color{red}987} \% \text{HASH\_SIZE}$
Modulo-Division Hashing
- นำ Key มา mod ด้วยขนาดของ Hash table index = key % HASH_SIZE;

Collision

การที่คนละ Key กันแต่หลังจาก Hash function ออกมา Index มีค่าเท่ากัน
จึงมีเทคนิคการหลบลีกค่าดังนี้
- Seperate chaining
  - เป็นการสร้าง Hash table ด้วย Array ของ Linked list
  - ถ้าหากมี Index ที่ซ้ำกันก็แค่ Insert last ของ Linked list นั้นไปเรื่อยๆ
- Open Address
  - Linear probing
    - เมื่อเกิดการ Collision ขึ้นจะเลื่อนตำแหน่งทีละ $1$ ไปเรื่อยจนกว่าจะเจอพื้นที่ว่าง / เจอค่า
  - Quadratic probing
    - เมื่อเกิดการ Collision จะเพิ่มตำแหน่งทีละ $i^2$ โดยที่ $i$ คือจำนวนครั้งที่เกิดการ Collision ในการหานั้นๆ
  - Double hashing
    - $index = (key + (i * hash2(key))) \% \text{HASH\_SIZE}$
    - $hash2(key) = R - (key \% R)$
    - โดยที่ $R$ มักจะเขียนว่า "Hash table สมมุติ"

Data structure เนื้อหามิดเทอม 2566/1

Table of Contents

Why should we learn Data structure?

Chapter 1 Data structure

Type of Data structure

Memory allocation

Type of problems

Complexity

Chapter 2 Stacks

What is a stack?

Constructor and Destructor

Stack Implementations

Stack Applications

Chapter 3 Queue

What is a queue?

Queue Implementations

Queue Applications

Chapter 4 Linked list

Static Allocation vs Dynamaic Allocation

Linked list Operations

Doubly linked list

Chapter 5 Hash table

Searhing

What is a hash table?

Hash function

Collision